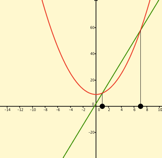
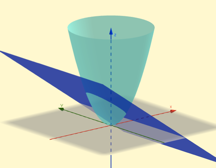
This paper is adapted from a paper written by the author and his colleague, Prof. Michal Yerushalmy of the University of Haifa in 1991. For several decades we[1] have been doing research on the nature of the cognitive map secondary mathematics teachers have of their subject, particularly in the areas of algebra, trigonometry and pre-calculus. We find it remarkably confused and incoherent, reflecting with great fidelity the confusion and the incoherence of the curricular materials that the teachers are generally asked to use in their teaching. Whatever else needs to be done to improve the teaching of mathematics in the secondary schools, and indeed there is much to be done, we believe that the content of the subject needs to be made more coherent and pedagogically workable. It is with this goal in mind and the experience of working closely with secondary teachers for many years that we present the following way of organizing thinking about the mathematics of function. We organize primary and secondary mathematics along two dimensions. These are mathematical objects and mathematical actions. Why? There are roughly 6 to 7 thousand languages spoken on Earth and they all, in one form or another, have nouns (objects) and actions (verbs). Given the level of universality of human thinking along the lines of objects and actions, it seems to us that there is merit in analyzing mathematics through that lens. Mathematical Objects The objects of school mathematics are numbers and quantities, shapes and spaces, patterns and functions[2], data and arrangements. In most countries the mathematics of number is the subject of early education. The mathematics of quantity[3] is not normally attended to in great detail in the elementary grades. Indeed, it is often more thoroughly explored in science classes than in mathematics classes. Most of our attention in the secondary grades is directed toward the mathematics of function [on domains such as R and R x R] and the mathematics of shape. We describe these subjects as analysis and geometry. We take the position, both mathematically and pedagogically, that the function[4] ought to be regarded as the primitive and fundamental object of analysis, i.e., the school subjects of algebra, trigonometry, probability and statistics, pre-calculus and calculus. In fact, we take a stronger position - we maintain that all the other constructs in the various secondary school mathematics subjects such as equations, inequalities, identities, relations, formulae, etc. can all be understood in terms of the fundamental object, i.e. the function. We focus on the following classes of functions as our mathematical objects; · Polynomials (e.g., constant, linear, quadratic, higher order) · power functions (integer & fractional powers) · periodic functions (e.g., trigonometric functions) · transcendental functions (exponential & logarithmic functions) · point functions (functions on discrete domains) · piecewise defined functions · shapes, spaces & constructions (functions on the domain of shapes) Mathematical Actions We consider the following set of mathematical actions; · Representing [symbolically & graphically] · Transforming symbolically [factoring, expanding,…] · Transforming graphically [scaling, translating, dilating, reflecting,…] · Transforming parametrically [f(a,b,…,x) ® f(a’,b’,…,x)] · Combining [binary operations on functions, including composition] · Unary operations [differentiation, integration,…] · Comparing [relations, equations & inequalities] Representing In a deep sense the most fundamental of all mathematical actions is representation. There are many ways to represent functions - two of the most powerful being the symbolically and graphically. These two representations are cognitively complementary. Each representation offers access to insights that is available only with difficulty in the other representation. We believe that students of mathematics should always work in environments where multiple representations of the functions they are working with are always, and simultaneously, available. Moreover, it should be possible to manipulate any representation of a function - sui generis - and see the consequences of one's action in other representations. Generally, plotting software allows users to manipulate symbolic representations symbolically and see the consequences graphically. Some of the software environments that we have developed and disseminated are among the relatively few available software environments that allow users to manipulate representations of functions – graphically - as well as symbolically. Transforming symbolically A good deal of instructional time in secondary mathematics subjects is spent in transforming functions, although it is often not recognized that that is the nature of the activity. It is clearly the case that all problems of the form "simplify", "factor", "expand", "collect similar terms" are instances of students being asked to transform the symbolic form of a function and re-express it in a different but equivalent form. Transforming graphically & Transforming parametrically Understanding the effect of graphical transformations such as scaling, translating, dilating and reflecting on functions of all sorts is crucial to the development of an appreciation of families of functions and to deepening one’s “function sense”[5] The same is true of transforming functions parametrically. Combining functions with binary operations As students grow in mathematical sophistication and come to regard functions as “objects” that are themselves subject to “actions” they discover that functions on the domain of numbers and quantities, functions on the domain of number and quantity pairs, and functions on shapes can be combined in many ways. Monomials can be added and subtracted to form polynomials, and infinite series of monomials can be used to define trigonometric and transcendental functions. Polynomials can be divided to form rational functions. Rotations, reflections and translations of shapes can be composed.[6] Unary operations on functions The study of calculus centers on understanding and developing facility with the two particular unary operations on functions that we call differentiation and integration. Comparing functions All problems of the form "solve" or "find the solution set of" are instances of a student being asked to write a given comparison of functions, i.e., an equation or inequality, as an equivalent comparison. For example the comparison of functions (an equation in this case) 8x + 2 = x2 + 9 can be transformed into a variety of equivalent forms one of which is | x - 4 | = 3 The equation 8x + 2 = x2 + 9 and its solution set {1,7} All these equivalent forms have the solution set x = {1,7}. This manipulation of comparisons of functions usually happens in a context in which the equation as a comparison of two objects called functions is, at best, ill-understood. What does it mean to say 8x + 2 = x2 + 9 Clearly 8x + 2 is not the same as x2 + 9. A functions approach in an environment in which both symbolic and graphical representations are present allows students to understand more readily what is meant by a "solution set" and to be able to view equations, identities and inequalities in a coherent fashion - all as examples of different kinds of comparisons of functions. The power of this approach is made further evident by the fact that all of the relations of analytic geometry can be understood as comparisons of functions of two variables. Thus, for example, the relation x2 + y2 = x - 4 which is normally depicted as an ellipse in the xy plane is now seen to be the comparison of two functions of two variables, i.e. F(x,y); x2 + y2 and G(x,y); x - 4 The graphical representation of the function F is a parabolic bowl [with circular cross-section], while the graphical representation of the function G is a plane [that intersects the xy plane along the line y = 4]. The projection of the intersection of these two surfaces on the xy plane is the ellipse that is usually plotted. It is not necessary to tell the usual story of the ellipse being "two functions"[7] The relation x2 + y2 = x - 4 The idea of constraining functions to be related to one another extends beyond the functions defined on numbers that form much of the content of school algebra. Indeed it lies at the heart of the application of calculus to modeling the world around us through differential equations. For example, differentiation is a function on the domain of functions that have the real numbers as their domain. Thus, given a function f(x), differentiating it yields a new function f’(x). Constraining f(x) to be proportional to f’(x) gives rise to a differential equation whose solution is a family of exponential functions. Here then is a way of organizing the mathematical content of the school subjects of analysis (algebra, trigonometry, pre- calculus, calculus) and geometry.
Object x Action Matrix [In most cells of the Object x Action matrix you will find one or more letters. These letters indicate in which of the nine challenge collections {a thru i} you are most likely to find a challenge germane to that cell. This mapping, from Object x Action to the organization of the challenge collections on this website is, of necessity, inadequate. No challenge can fix neatly and exactly into only one cell in this matrix. Every challenge will lie in several, perhaps even many, cells. By the same token, every cell in the matrix will, in all likelihood, be germane to many challenges. Nonetheless...]
[1] The author is deeply indebted to his colleagues and to the many teachers and students with whom he has worked over the years. [2] A first encounter with the concept of function leads naturally to thinking of functions as “actions” or processes carried out on numbers, quantities and shapes rather than objects. As one’s sophistication grows, one comes to appreciate the fact that the function itself can indeed be regarded as an “object” and that there are actions that can be carried out on them. [3] See, “Semantic Aspects of Quantity” (on this website) for further explication of the mathematics of quantity. [4] The concept of function entails the concept of variable and vice versa [5] See essay “Developing Function Sense” on this web site. [6] Going further, the process continues – collection of functions with defined properties can be combined to form still more complex “objects” such as groups. [7] The ellipse (x/a)2 + (y/b)2 = 1 is normally regarded as a relation involving two variables. In order to plot this relation in the xy plane students are taught to solve for y, thereby obtaining the two functions of one variable b[1 - (x/a)2]1/2 and -b[1 - (x/a)2]1/2 It should also be noted that the traditional graphical representation in analytic geometry of the slicing of the cone by a plane involves not the quadratic function F(x,y): x2+y2 but rather the function F(x,y): [x2+y2]1/2. |